HTML5 Canvas: матричные преобразования

Последнее обновление 31 июля 2019 11:49:42 (UTC / GMT +8 часов)

script1adsense2code

script1adsense3code

Вступление

Вращение, перемещение и масштабирование выполняются с использованием матрицы преобразования - набора из девяти чисел, которые используются для преобразования двумерного массива, такого как растровое изображение, с использованием линейной алгебры. Математически все преобразования можно представить в виде матриц преобразования 3х3 следующего вида:

Поскольку в вышеуказанной матрице 3x3 используются только шесть значений, матрица преобразования также выражается в виде вектора: [abcdef].

Преобразование координат и длин карт из новой системы координат в предыдущую систему координат

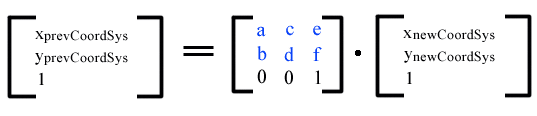
Простые преобразования представлены в виде матрицы следующим образом:

Перевод эквивалентен матрице -

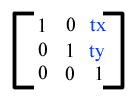
или [1 0 0 1 tx ty], где tx и ty - расстояния для перевода координат в X и Y соответственно.

Масштабирование эквивалентно матрице -

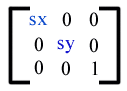
: или [sx 0 0 sy 0 0], Одна единица в направлениях X и Y в новой системе координат равна единице sx и sy в предыдущей системе координат соответственно.

Вращение о происхождении эквивалентно матрице -

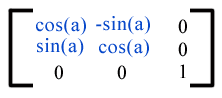
или [cos (a) sin (a) -sin (a) cos (a) 0 0]), что приводит к повороту осей системы координат на угол a.

Перекосное преобразование вдоль оси x эквивалентно матрице -

или [1 0 tan (a) 1 0 0], что приводит к перекосу координат X на угол a.

Перекосное преобразование вдоль оси y эквивалентно матрице -

Вы можете изменить исходную точку (0,0) поверхности рисования, вызвав метод translate (x, y). Начало координатной системы холста перемещается в точку (x, y). Используя метод контекста rotate (angle), вы можете вращать систему координат холста вокруг его начала. Система координат вращается на угол радианы по часовой стрелке. На все, что уже есть на холсте, это не влияет, но последующие операции рисования поворачиваются. Преимущество этих методов заключается в том, что при масштабировании будет использоваться не просто несколько пикселей.
Эти базовые методы преобразования фактически являются аффинными преобразованиями , рассчитанными с помощью матриц, причем каждое новое преобразование приносит новое преобразование в предыдущую матрицу. Вы можете определить свои собственные матрицы следующим образом.

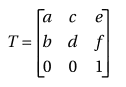
Это делается одним из следующих способов:

преобразование (a, b, c, d, e, f)
setTransform (a, b, c, d, e, f)

Примечание. Аргументы a, b, c, d, e и f иногда называют m11, m12, m21, m22, dx и dy или m11, m21, m12, m22, dx и dy.

метод transform ()

Метод transform () используется для изменения матрицы преобразования текущего контекста.

Синтаксис:

 ctx .transform (m11, m12, m21, m22, dx, dy)

параметры	Тип	Описание
m11	число	Значение m1,1 в матрице. [Увеличивает или уменьшает размер пикселей по горизонтали.]
m12	число	Значение m1,2 в матрице. [Это эффективно наклоняет ось X вверх или вниз.]
m21	число	Значение m2,1 в матрице. [Это эффективно наклоняет ось Y влево или вправо.]
m22	число	Значение m2,2 в матрице. [Увеличивает или уменьшает размер пикселей по вертикали.]
дх	число	Значение дельты x (dx) в матрице. [Перемещает всю систему координат по горизонтали]
ду	число	Значение дельты y (dy) в матрице. [Перемещает всю систему координат по вертикали.]

метод setTransform ()

Метод setTransform (a, b, c, d, e, f) сбрасывает текущее преобразование в единичную матрицу, а затем вызывает метод transform (a, b, c, d, e, f) с теми же аргументами.

Синтаксис:

 ctx .setTransform (m11, m12, m21, m22, dx, dy)

параметры	Тип	Описание
m11	число	Значение m1,1 в матрице. [Увеличивает или уменьшает размер пикселей по горизонтали.]
m12	число	Значение m1,2 в матрице. [Это эффективно наклоняет ось X вверх или вниз.]
m21	число	Значение m2,1 в матрице. [Это эффективно наклоняет ось Y влево или вправо.]
m22	число	Значение m2,2 в матрице. [Увеличивает или уменьшает размер пикселей по вертикали.]
дх	число	Значение дельты x (dx) в матрице. [Перемещает всю систему координат по горизонтали]
ду	число	Значение дельты y (dy) в матрице. [Перемещает всю систему координат по вертикали.]

Мы уже обсуждали, вращение, перемещение и масштабирование выполняются с использованием матрицы преобразования. Смотрите следующие два примера, каждый пример нарисует похожий прямоугольник:

Пример - 1:
Следующий веб-документ рисует прямоугольник с помощью метода transform ():

Выход:

Код:

<!DOCTYPE html>
<html>
<head>
<title>Matrix Transforms</title>
</head>
<body>
<canvas id="DemoCanvas" width="300" height="400"></canvas>
<script>
var canvas = document.getElementById("DemoCanvas");
if (canvas.getContext) 
{
 var ctx = canvas.getContext('2d');
 ctx.beginPath();  
 ctx.lineWidth ="3";  
 var cos=Math.cos(45*Math.PI / 180);
 var sin=Math.cos(45*Math.PI / 180);
 ctx.transform(cos, sin, -sin, cos, 160, 20); 
 ctx.strokeStyle ="red";  
 ctx.strokeRect(60, 60, 160, 160);  
 ctx.stroke();   
}
</script>
</body> 
</html>

Пример - 2:
Следующий веб-документ рисует аналогичный прямоугольник предыдущего примера с использованием методов translate () и rotate ():

Выход:

Код:

<!DOCTYPE html>
<html>
<head>
<title>Matrix Transforms and translate() and rotate() methods</title>
</head>
<body>
<canvas id="DemoCanvas" width="300" height="400"></canvas>
<script>
var canvas = document.getElementById("DemoCanvas");
if (canvas.getContext) 
{
 var ctx = canvas.getContext('2d');
 ctx.beginPath();  
 ctx.translate(160, 20);   
 ctx.rotate(45*Math.PI / 180);
 ctx.strokeStyle ="red";  
 ctx.strokeRect(60, 60, 160, 160);  
 ctx.stroke();   
}
</script>
</body> 
</html>

Установка матрицы для отражения

Вызывая метод ctx.setTransform (1, 0, 0, -1, 0, 0), вы можете настроить матрицу преобразования так, чтобы она отражала все вокруг оси y. Поэтому все операции рисования приводят к перевернутому изображению, и все координаты y умножаются на -1.

Вызывая метод ctx.setTransform (-1, 0, 0, 1, 0, 0), вы можете настроить матрицу преобразования так, чтобы она отражала все вокруг оси x. Поэтому все операции рисования приводят к зеркальному отображению, а все x-координаты умножаются на -1.

В следующем примере весь текст отражается вокруг оси Y.

Выход :

Код:

<!DOCTYPE html>
<html>
<head>
<title>Matrix Transforms</title>
</head>
<body>
<canvas id="DemoCanvas" width="300" height="400"></canvas>
<script>
var canvas = document.getElementById("DemoCanvas");
if (canvas.getContext) 
{
 var ctx = canvas.getContext('2d');
 ctx.beginPath();  
 ctx.lineWidth ="3";  
 var cos=Math.cos(45*Math.PI / 180);
 var sin=Math.cos(45*Math.PI / 180);
 ctx.transform(cos, sin, -sin, cos, 160, 20); 
 ctx.strokeStyle ="red";  
 ctx.strokeRect(60, 60, 160, 160);  
 ctx.stroke();   
}
</script>
</body> 
</html>

Пример: эллипс

В следующем примере рисуется эллипс, в котором использовался метод transform (), и масштабируем холст в соответствующем направлении, чтобы круг становился эллипсом.

Выход:

Код:

<!DOCTYPE html>
<html>
<head>
<title>Matrix Transforms - ellipse</title>
</head>
<body>
<canvas id="DemoCanvas" width="300" height="400"></canvas>
<script>
var canvas = document.getElementById("DemoCanvas");
if (canvas.getContext) 
{
 var ctx = canvas.getContext('2d');
 ctx.transform(1.6,0,0,1,0,0);
 ctx.beginPath();
 ctx.fillStyle ='red';
 ctx.lineWidth = 4;
 ctx.arc(60, 60, 45, 0, 2 * Math.PI, true);
 ctx.stroke();
 ctx.fill();  
}
</script>
</body> 
</html>

Редактор кода:

См. Общий редактор Pen html css от w3resource ( @ w3resource ) в CodePen .

Предыдущий: HTML5 Canvas перевод, масштабирование и вращение учебник
Далее: HTML5 Canvas: композитинг