Python Math: вычисление квадратных корней с использованием вавилонского метода

Python Math: Упражнение-18 с решением

Напишите программу на Python для вычисления квадратных корней с помощью вавилонского метода.

Возможно, первый алгоритм, используемый для аппроксимации √S, известен как вавилонский метод, названный в честь вавилонян, или «метод Героя», названный в честь греческого математика первого столетия Героя Александрийского, который дал первое явное описание метода. Это может быть получено из (но предшествует 16 векам) метода Ньютона. Основная идея состоит в том, что если x является завышенным значением для квадратного корня неотрицательного действительного числа S, то S / x будет заниженным, и поэтому можно ожидать, что среднее из этих двух чисел обеспечит лучшее приближение.

График презентации

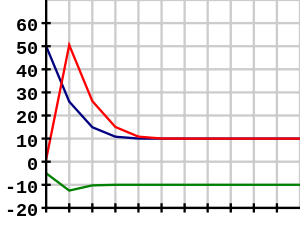
График показывает использование вавилонского метода для аппроксимации квадратного корня из 100 (10) с использованием начальных значений x0 = 50, x0 = 1 и x0 = −5. Обратите внимание, что использование отрицательного начального значения дает отрицательный корень.
График Авторы : Crotalus Horridus

Пример решения : -

Код Python:

def BabylonianAlgorithm(number):
    if(number == 0):
        return 0;
    g = number/2.0;
    g2 = g + 1;
    while(g != g2):
        n = number/ g;
        g2 = g;
        g = (g + n)/2;
    return g;
print('The Square root of 0.3 =', BabylonianAlgorithm(0.3));

Пример вывода:

 Квадратный корень 0,3 = 0,5477225575051661 

Блок - схема:

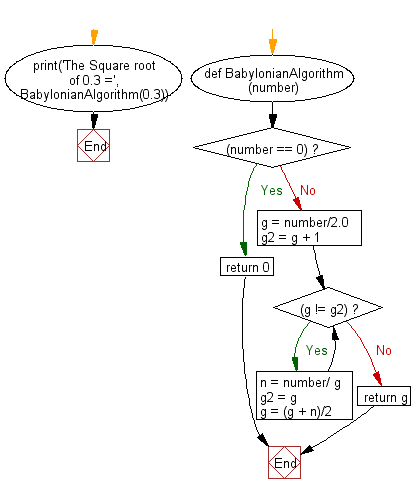
Визуализируйте выполнение кода Python:

Следующий инструмент визуализирует, что компьютер делает шаг за шагом при выполнении указанной программы:

Редактор кода Python:

Есть другой способ решить это решение? Внесите свой код (и комментарии) через Disqus.

Предыдущий: Напишите программу на Python для печати первых n счастливых чисел.
Далее: Напишите программу на Python для умножения двух целых чисел без использования оператора * в Python.