Упражнения на Java: классифицируйте обильные, недостающие и совершенные числа (целые числа) от 1 до 10000

Номера Java: Упражнение-2 с решением

Напишите программу на Java, чтобы классифицировать «обильные», «несовершенные» и «совершенные» числа (целые числа) от 1 до 10000.

В теории чисел обильное число - это число, для которого сумма его собственных делителей больше, чем само число.
Пример :
Первые несколько чисел:
12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100, 102,…
Целое число 12 является первым обильным числом. Его правильными делителями являются 1, 2, 3, 4 и 6, всего 16.
Дефицитное число. В теории чисел дефектное число - это число n, для которого сумма делителей σ (n) <2n или, что эквивалентно, сумма собственных делителей (или аликвотной суммы) s (n) <n. Значение 2n - σ (n) (или n - s (n)) называется дефицитом числа.
Например, делителями 21 являются 1, 3 и 7, а их сумма равна 11. Поскольку 11 меньше 21, число 21 является дефицитным. Его дефицит составляет 2 × 21 - 32 = 10.
Первые несколько недостатков:
1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 19, 21, 22, 23, 25, 26, 27, 29, 31, 32, 33, …….
Совершенное число. В системе счисления совершенное число - это положительное целое число, равное сумме его собственных положительных делителей, то есть суммы его положительных делителей, исключая само число.
Эквивалентно, совершенное число - это число, которое является половиной суммы всех его положительных делителей (включая себя), т.е. σ1 (n) = 2n.
Первое совершенное число - 6. Его правильные делители - 1, 2 и 3, и 1 + 2 + 3 = 6. Эквивалентно, число 6 равно половине суммы всех его положительных делителей: (1 + 2 + 3 + 6) / 2 = 6. Следующее совершенное число - 28 = 1 + 2 + 4 + 7 + 14. За ним следуют совершенные числа 496 и 8128.

Иллюстрированная презентация:

Пример решения:

Java-код:

import static java.util.stream.LongStream.rangeClosed;
public class Exercise2 {
    
   public static void main(String[] args) {
        int count_Deficient_no = 0;
        int count_Perfect_no = 0;
        int count_Abundant_no = 0;
 
        for (long i = 1; i <= 10_000L; i++) {
            long sum = proper_Divs_Sum(i);
            if (sum < i)
                count_Deficient_no++;
            else if (sum == i)
                count_Perfect_no++;
            else
                count_Abundant_no++;
        }
        System.out.println("Number Counting [(integers) between 1 to 10,000]: ");
        System.out.println("Deficient number: " + count_Deficient_no);
        System.out.println("Perfect number: " + count_Perfect_no);
        System.out.println("Abundant number: " + count_Abundant_no);
    }
     public static Long proper_Divs_Sum(long num) {
        return rangeClosed(1, (num + 1) / 2).filter(i -> num % i == 0 && num != i).sum();
    }
}

Пример вывода:

 Подсчет чисел [(целые числа) от 1 до 10000]:                                                             
Номер дефекта: 7508                                                                                        
Идеальный номер: 4                                                                                             
Обильный номер: 2488

Блок - схема:

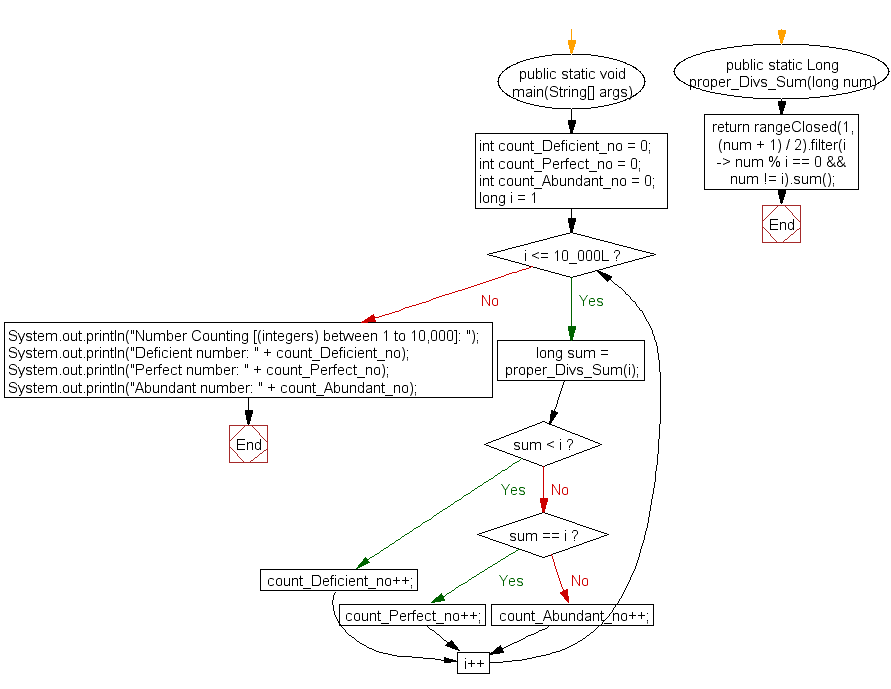
Редактор кода Java:

Внесите свой код и комментарии через Disqus.

Предыдущий: Напишите программу на Java, чтобы проверить, является ли данное число уродливым числом.
Далее: написать программу на Java для генерации случайных целых чисел в определенном диапазоне.