Упражнения на Java: докажите, что алгоритм Евклида вычисляет наибольший общий делитель двух положительных целых чисел

Java Basic: упражнение 157 с решением

Напишите программу на Java, чтобы доказать, что алгоритм Евклида вычисляет наибольший общий делитель двух положительных целых чисел.

Согласно Википедии «Евклидов алгоритм основан на том принципе, что наибольший общий делитель двух чисел не изменяется, если большее число заменяется его разностью на меньшее число. Например, 21 - это GCD из 252 и 105 (как 252 = 21 × 12 и 105 = 21 × 5), и то же число 21 также является GCD 105 и 252 - 105 = 147. Поскольку эта замена уменьшает большее из двух чисел, повторение этого процесса дает последовательно меньшие пары числа до тех пор, пока два числа не станут равными. Когда это происходит, они представляют собой GCD исходных двух чисел. В обратном порядке шаги GCD могут быть выражены в виде суммы двух исходных чисел, каждое из которых умножено на положительное или отрицательное целое число, например , 21 = 5 × 105 + (−2) × 252. Тот факт, что GCD всегда можно выразить таким образом, известен как тождество Безу ».

Иллюстрированная презентация:

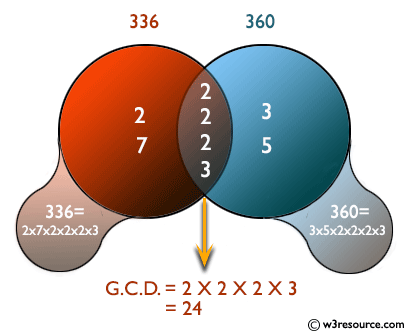
Пример решения:

Java-код:

import java.util.Scanner;
public class Solution {
	public static int euclid(int x, int y) {
		if (x == 0 || y == 0) {
			return 1;
		}
		if (x < y) {
			int t = x;
			x = y;
			y = t;
		}
		if (x % y == 0) {
			return y;
		} else {
			return euclid(y, x % y);
		}
	}
	public static void main(String[] args) {
		System.out.println("result: " + euclid(48, 24));
		System.out.println("result: " + euclid(125463, 9658));
	}
}

Пример вывода:

 результат: 24
результат: 1

Блок - схема:

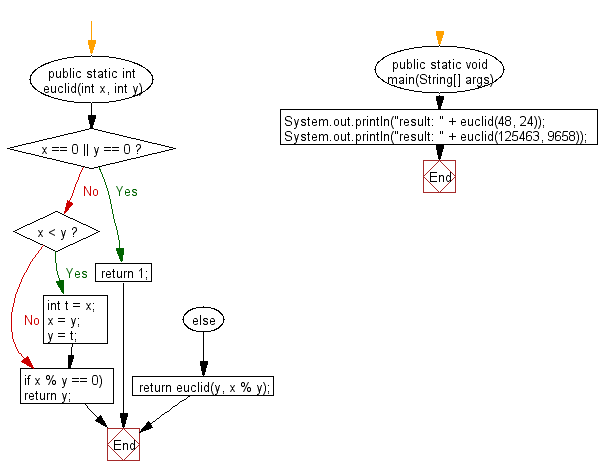
Редактор кода Java:

Внесите свой код и комментарии через Disqus.

Предыдущий: Напишите программу на Java, которая возвращает наибольшее целое число, но не больше, чем логарифм с целым числом 2 для данного целого числа.
Далее: Напишите программу на Java для создания двумерного массива (mxm) A [] [] так, чтобы A [i] [j] было истинным, если I и j простые и не имеют общих множителей, в противном случае A [i] [ J] становится ложным.